REVISION NOTES
IGCSE Edexcel Mathematics A
3.1 Sequences
3.1.1 Generate terms of a sequence using term-to-term and position-to-term definitions of the sequence
- A sequence is an systematic set of (most of the time) numbers
- Each of the numbers in the sequence is called a term
- The location of a term within a sequence is called its position. (eg. n is an unknown position
- For the first term, n=1 and for the second term, n=2, and so on
- Subscript notation is used to talk about a particular term
- a1 would be the first term in a sequence
- a7 would be the seventh term
- an would be the nth term
- A position-to-term rule gives the nth term of a sequence in terms of n
- This is a very powerful piece of mathematics
- With a position-to-term rule the 100th term of a sequence can be found without having to know or work out the first 99 terms!
- A term-to-term rule gives the (n+1)th term in terms of the nth term
- ie an+1 is given in terms of an
- If a term is known, the next one can be worked out
How do I use a position-to-term rule to write the first n terms of a sequence?
- To generate the first n terms of a sequence using a position-to-term rule (an nth term rule), substitute n = 1, n = 2, n = 3, and so on, into the rule
- For example, using an = 2n + 3 to generate the first four terms;
- 1st term: n = 1 so a1 = 2(1) + 3 = 5
- 2nd term: n = 2 so a2 = 2(2) + 3 = 7
- 3rd term: n = 3 so a3 = 2(3) + 3 = 9
- 4th term: n = 4 so a4 = 2(4) + 3 = 11
- Sequence is 5, 7, 9, 11, …
- Another example, using an = n2 − 5 to generate the first four terms;
- a1 = 12 − 5 = -4
- a2 = 22 − 5 = -1
- a3 = 32 − 5 = 4
- a4 = 42 − 5 = 11
- Sequence is -4, -1, 4, 11, … (This is an example of a quadratic sequence)
How do I use a term-to-term rule to write the first n terms of a sequence?
- To generate the first n terms of a sequence using a term-to-term rule (an nth term rule), you need to be given the first term (a1) and the term-to-term rule
- The term-to-term rule may be given in the form “an+1 = … ” where an+1 means the next term
- For example, a1 = 5 and an+1 = an + 2, generate the first four terms;
- 1st term, a1 = 5
- 2nd term, a2 = a1 + 2 = 5 + 2 = 7
- 3rd term, a3 = a2 + 2 = 7 + 2 = 9
- 4th term, a4 = a3 + 2 = 9 + 2 = 11
- Sequence is 5, 7, 9, 11, … Notice that this is the same sequence that was generated above using the position-to-term rule an = 2n + 3
- Another example, a1 = 5 and an+1 = 2an, generate the first four terms;
- a1 = 5
- a2 = 2a1 = 2 × 5 = 10
- a3 = 2a2 = 2 × 10 = 20
- a4 = 2a4 = 2 × 20 = 40
- Sequence is 5, 10, 20, 40, … (This is an example of a geometric sequence)
- A final example, a1 = 1, a2 = 1 and an+2 = an+1 + an, generate the first four terms;
- a1 = 1 and a2 = 1
- a3 = a2 + a1 = 1 + 1 = 2
- a4 = a3 + a2 = 2 + 1 = 3
- a5 = a4 + a3 = 3 + 2 = 5
- Sequence is 1, 1, 2, 3, 5, … (This is the Fibonacci sequence)


3.1.2 Find subsequent terms of an integer sequence and the rule for generating it
3.1.3 Use linear expressions to describe the nth term of arithmetic sequences
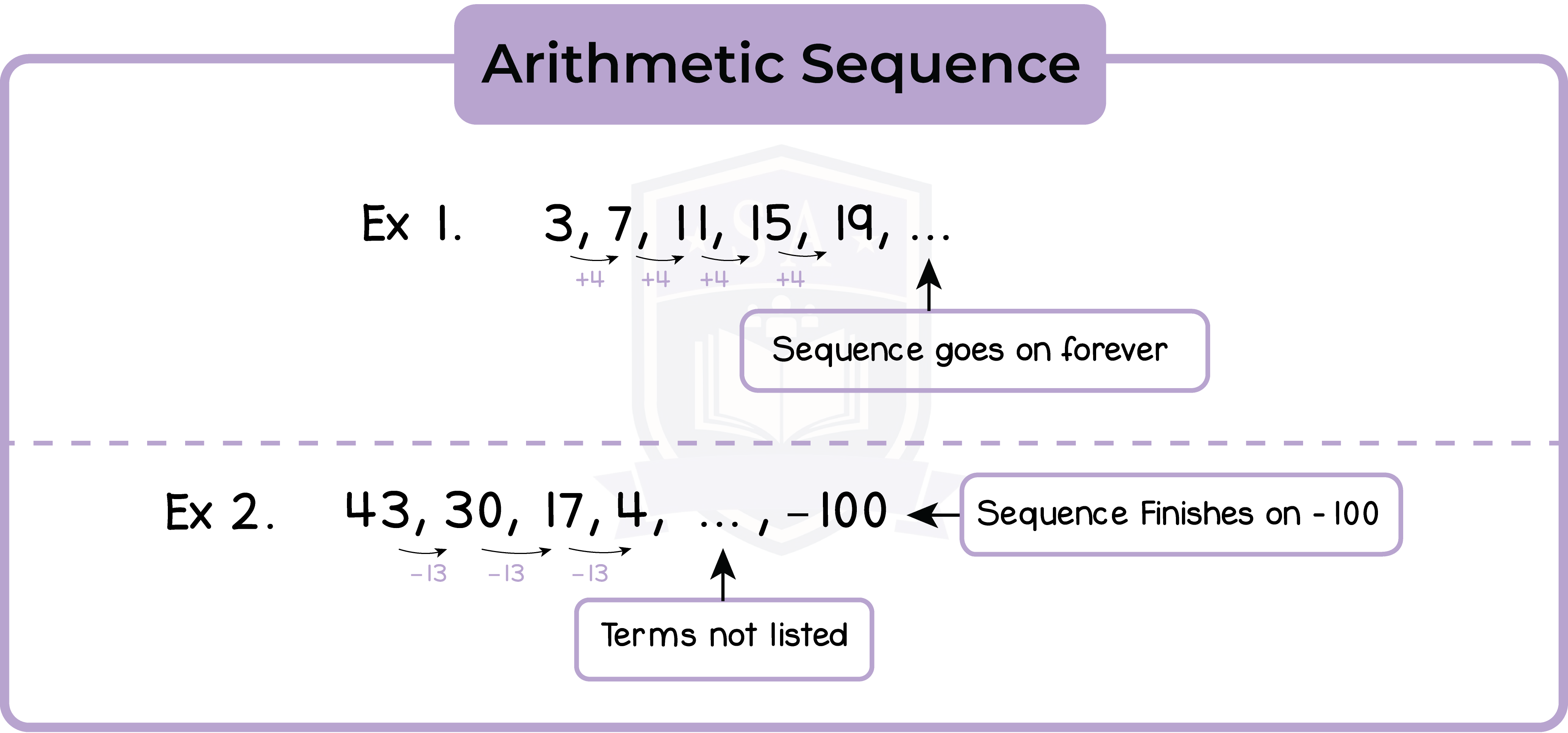
3.1.4 Understand and use common difference (d) and first term (a) in an arithmetic sequence (Higher Tier Only)

3.1.5 Know and use nth term = a + (n – 1) d (Higher Tier Only)
3.1.6 Find the sum of the first n terms of an arithmetic series (Sn) (Higher Tier Only)



