REVISION NOTES
IGCSE Edexcel Mathematics A
5.1 Vectors (Higher Tier Only)
5.1.1 Understand that a vector has both magnitude and direction (Higher Tier Only)
A vector is a quantity that has a magnitude (length) and a direction.
Example: Displacement, velocity and acceleration.


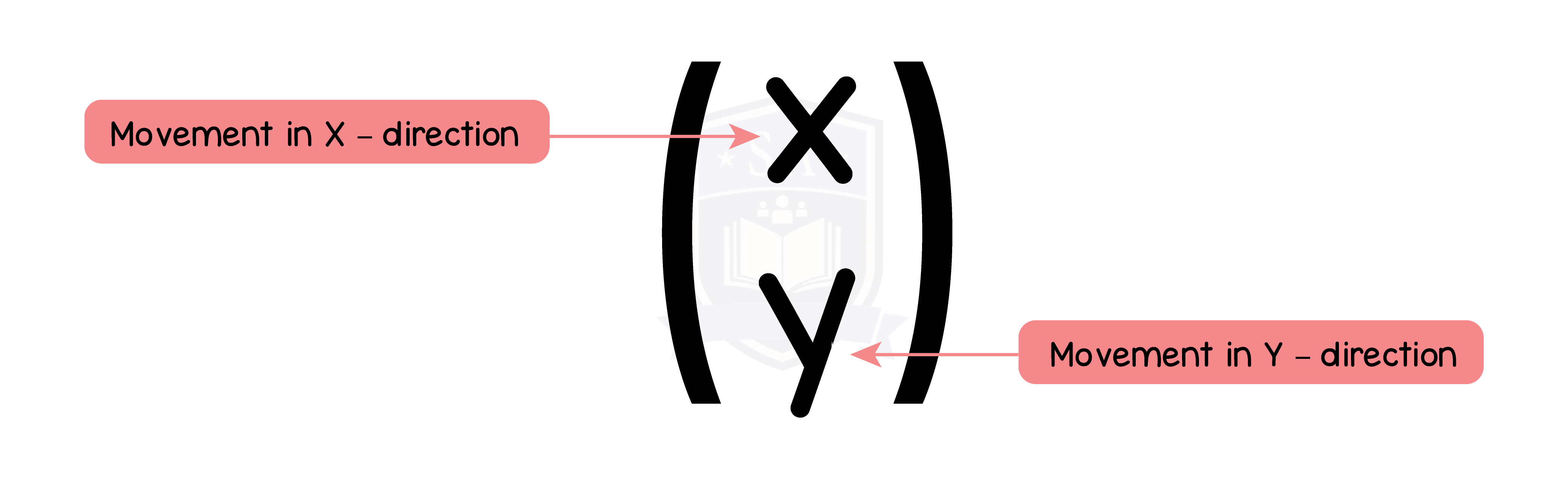
5.1.2 Understand and use vector notation including column vectors (Higher Tier Only)
Vectors are often described using column vector.
Vectors are often named using letter a, b, c, etc.
The letters are usually underlined if written by hand, but they are in bold type in examination papers.
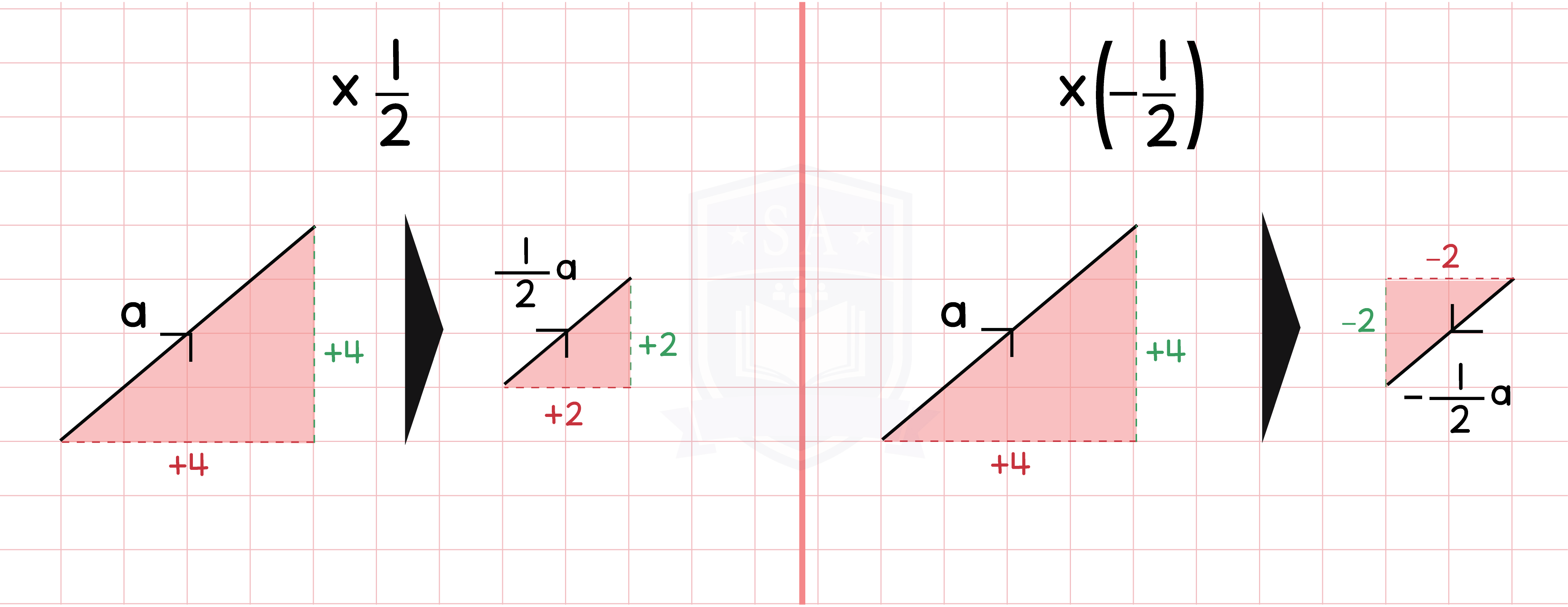
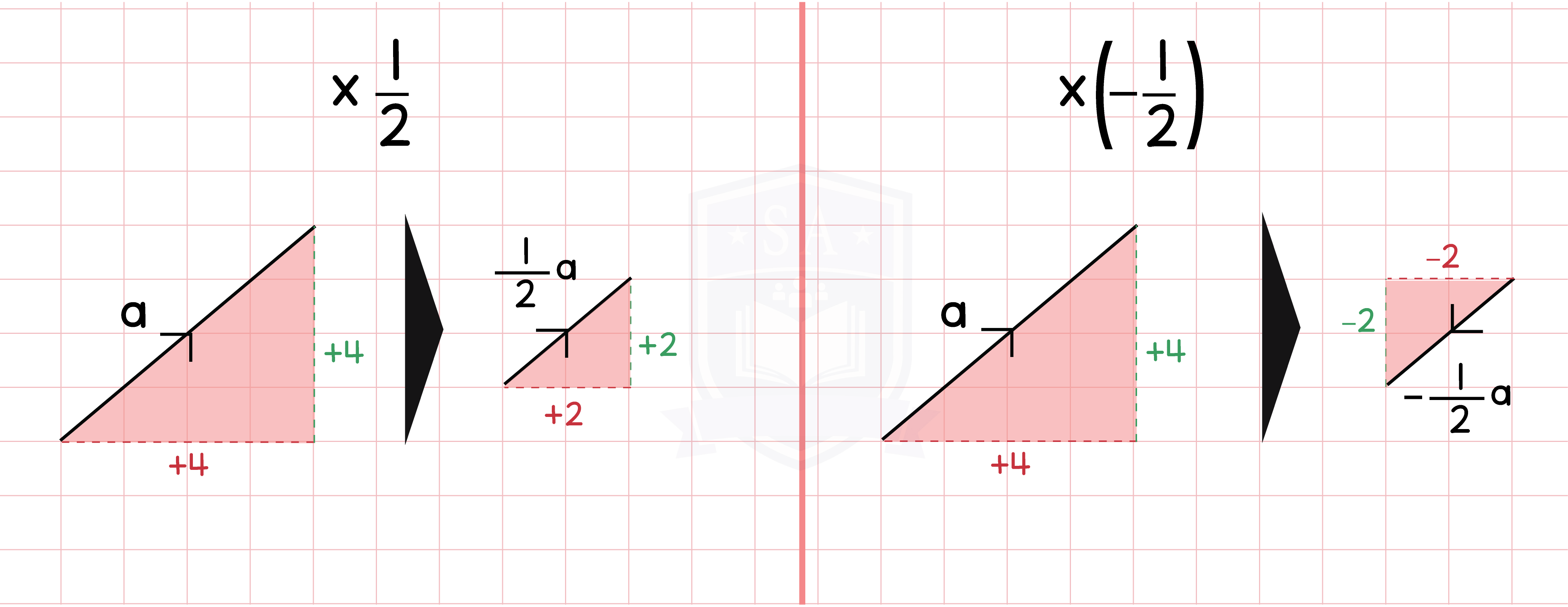
5.1.3 Multiply vectors by scalar quantities (Higher Tier Only)
When you multiply a vector by an ordinary number, k:
- The direction of the vector remains unaltered
- The magnitude is changed by factor k
To find he negative of a vector, reverse the sign of the numbers.

5.1.4 Add and subtract vectors (Higher Tier Only)
You can add and subtract two vectors using simple arithmetic.
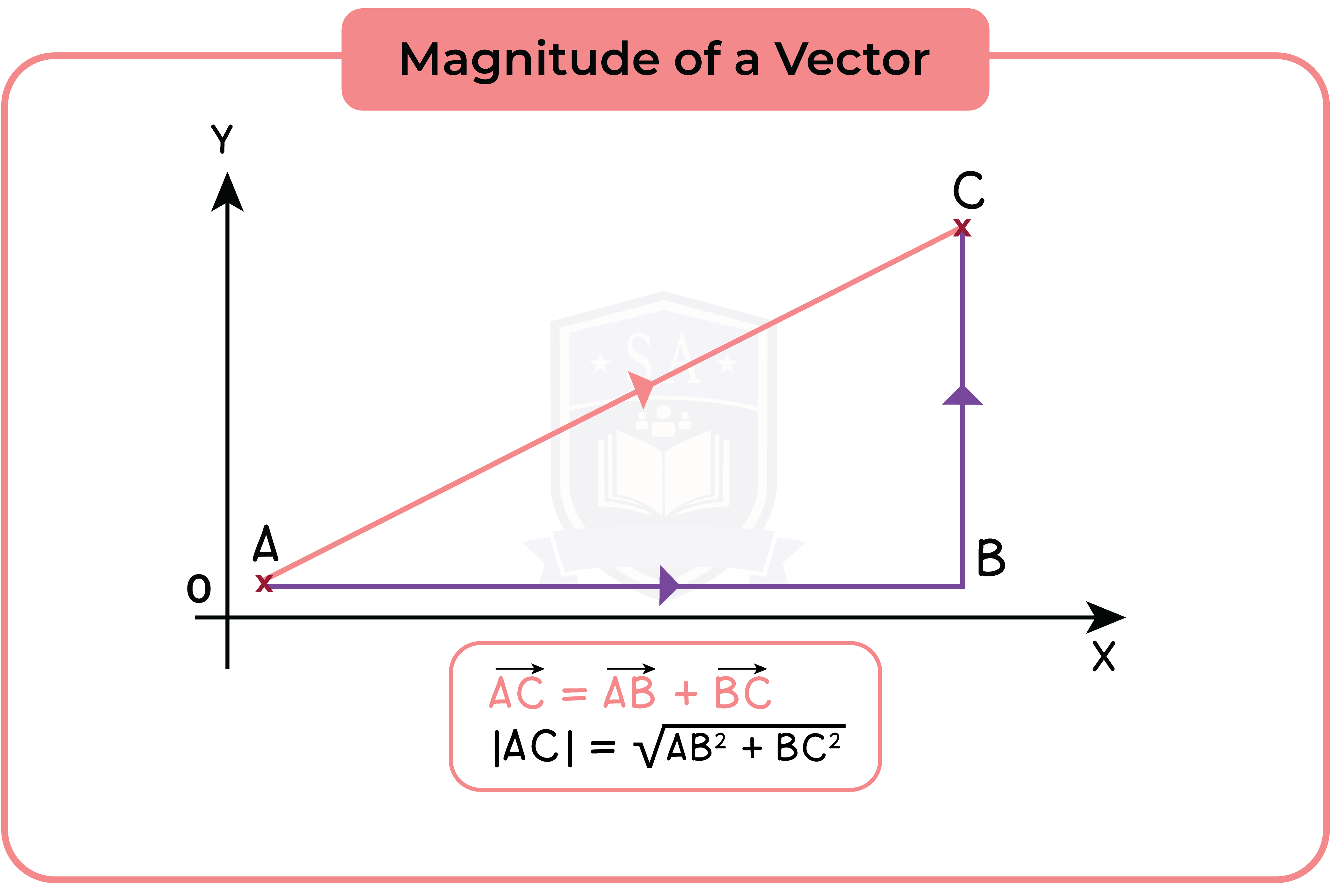
5.1.5 Calculate the modulus (magnitude) of a vector (Higher Tier Only)
The magnitude of a is the length.
We can use Pythagoras’ theorem to find it.
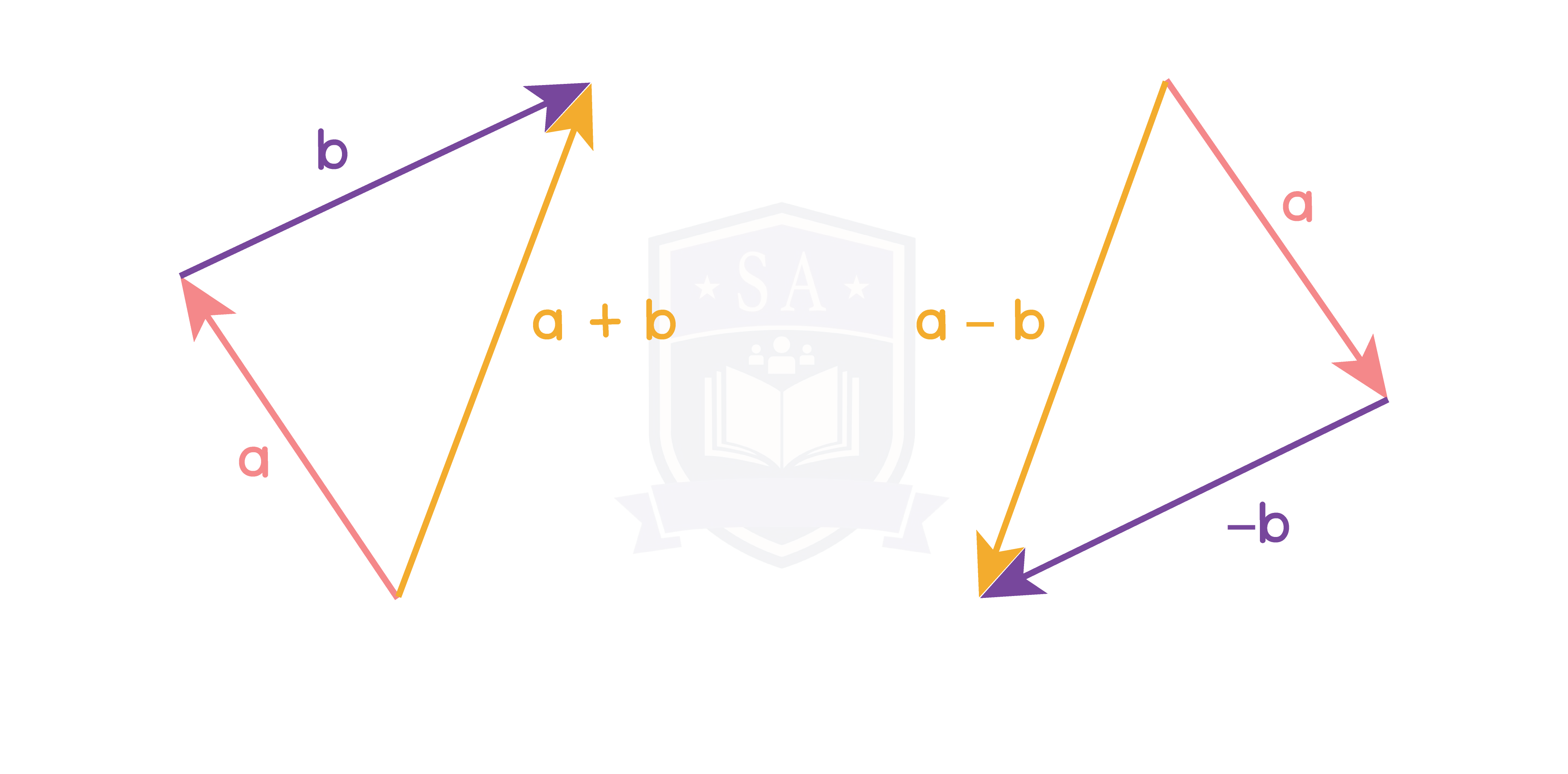
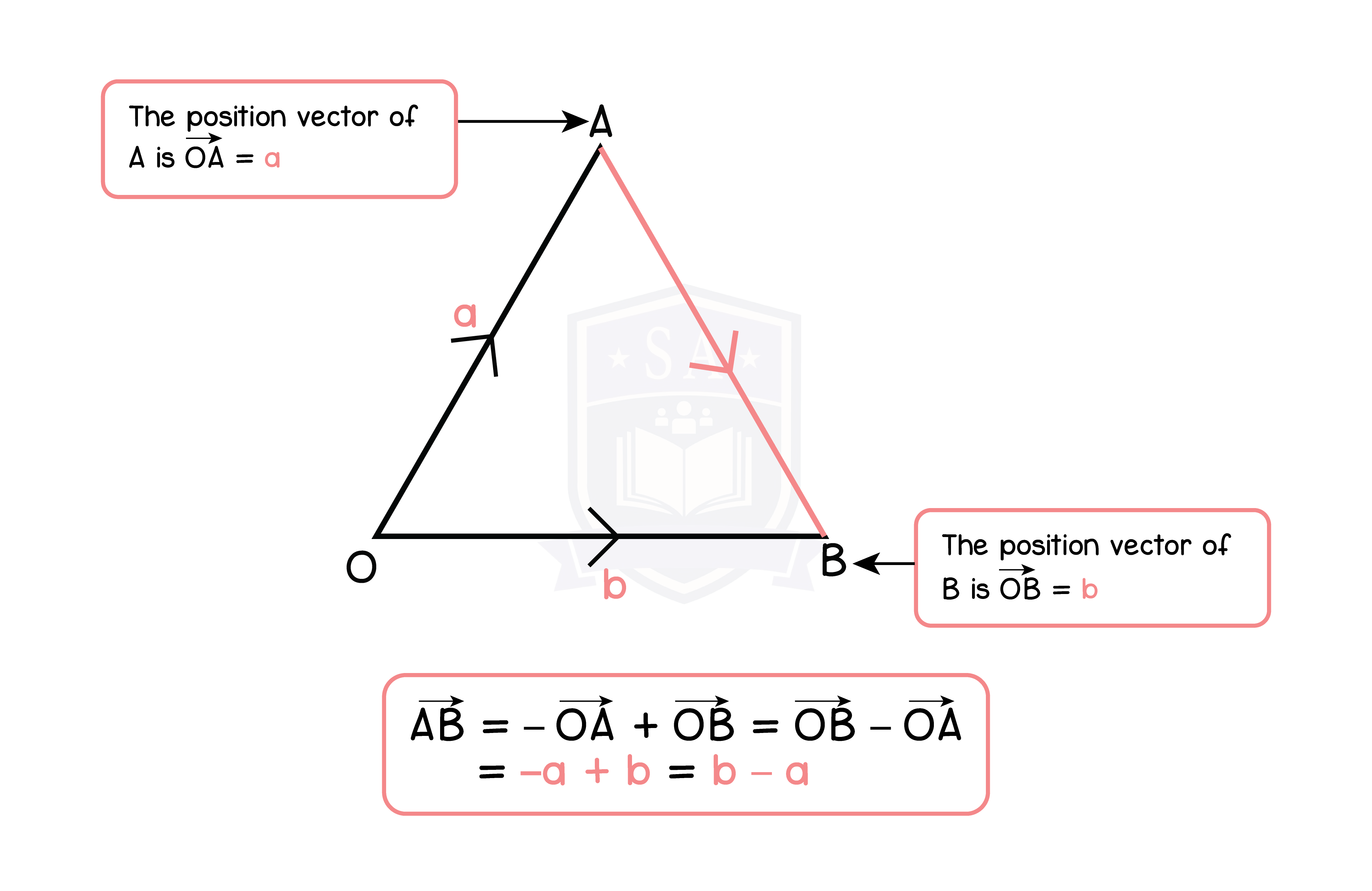
5.1.6 Find the resultant of two or more vectors (Higher Tier Only)
AB = AO + OB
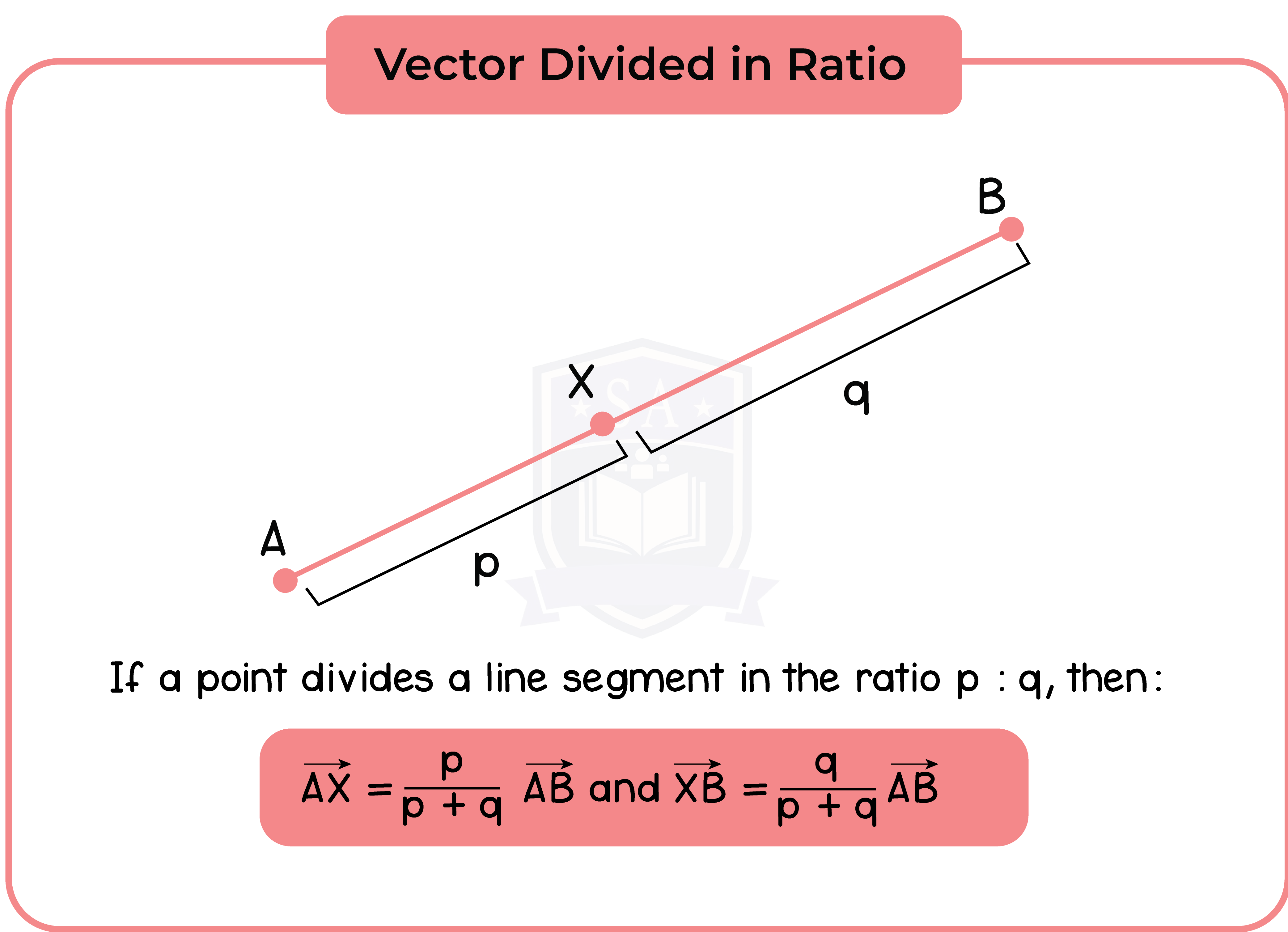
Ratio and Vectors:
If X is the point on AB for which AX : XB = 2 : 1, this means that AX is twice as long as XB.
Therefore, AX is two-thirds of the way along AB.



5.1.7 Apply vector methods for simple geometrical proofs (Higher Tier Only)
Proof 1: Parallel Line
Condition: If AB = k CD, AB and CD are parallel.
For example, 6a + 3b is parallel to 2a + b, since 6a + 3b = 3 x (2a + b)
Proof 2: Straight Line
Condition 1: If AB = k CD, AB and CD are parallel.
Condition 2: Since both AB and BC go through common point B, therefore ABC is a straight line.

